高等数学学习笔记

第一章 极限与连续

1.1 函数

1.1.1 基本概念

1. 函数: 定义域内总有唯一的y对应x

2. 复合函数: 设$u=φ(x)(x∈D_1)$,$y=f(u)(u∈D_2)$,对于任意$x∈D_1$,有$φ(x)∈D_2$,则y为x的复合函数，记作$y=f(φ(x))$

3. 反函数: 设$y=f(x)$为单调函数,$x∈D$,$y∈R$,若对于任意$y∈R$,有唯一的$x∈D$,使得$f(x)=y$,则称x是y的反函数，记作$x=f^{-1}(y)$

4. 基本初等函数:

• 幂函数: $y=x^a(a∈R)$
• 指数函数: $y=a^x(a>0,a≠1)$
• 对数函数: $y=log_a x(a>0,a≠1)$
• 三角函数: $y=sin x,y=cos x,y=tan x,y=cot x,y=sec x,y=csc x$
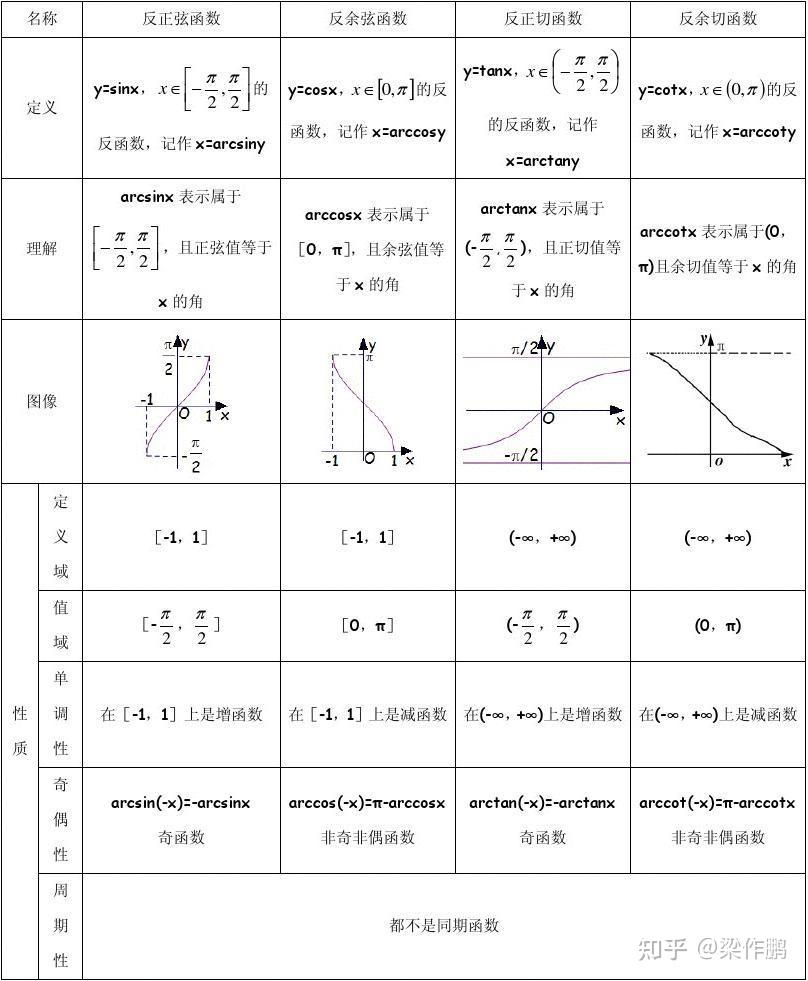
• 反三角函数: $y=arcsin x,y=arccos x,y=arctan x,y=arccot x,y=arcsec x,y=arccsc x$

---

三角函数复习

1. 三角函数图象和性质

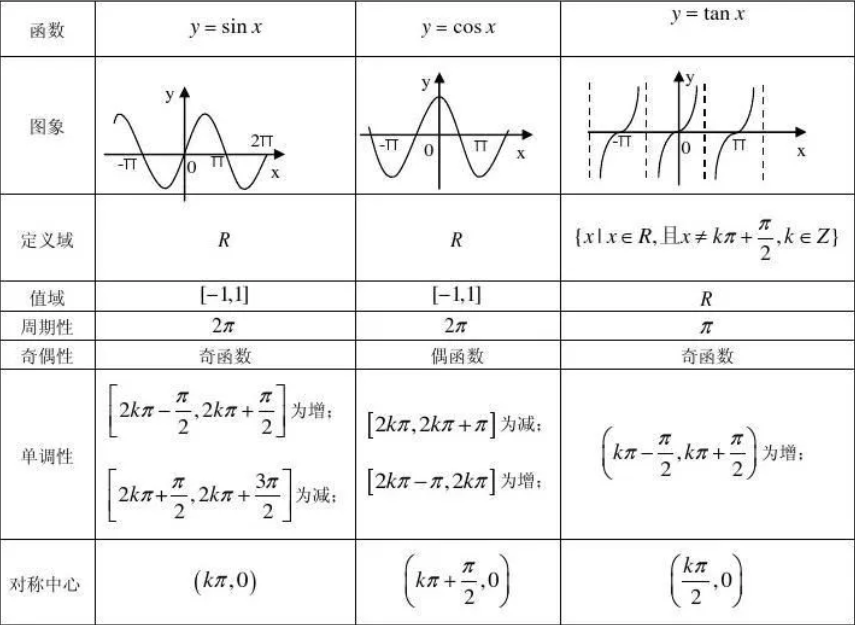
函数	$y=cotx$	$y=secx$	$y=cscx$
图象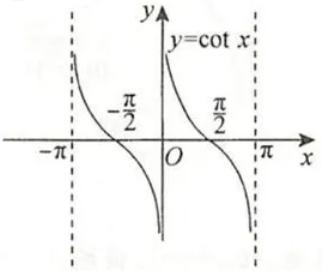
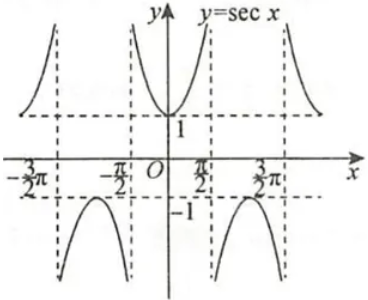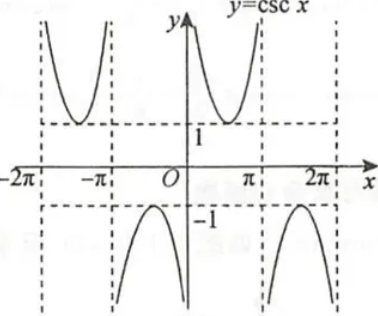定义域	$x≠kπ(k∈Z)$	$x≠\frac{π}{2}+kπ(k∈Z)$	$x≠kπ(k∈Z)$
值域	$(-∞,∞)$	$(-∞,-1]∪[1,∞)$	$(-∞,-1]∪[1,∞)$
周期性	$π$	$2π$	$2π$
奇偶性	奇函数	偶函数	奇函数
单调性	$(kπ,kπ+π)$为减	$[2kπ,2kπ+\frac{π}{2})∪(2kπ+\frac{π}{2})$为增，$(2kπ+π,2kπ+\frac{3π}{2})∪[2kπ+\frac{3π}{2}，2π+2kπ)$为减	$[2kπ+\frac{π}{2},2kπ+π)∪(2kπ+π,2kπ+\frac{3π}{2})$为增，$[2kπ-\frac{π}{2},2kπ)∪(2kπ，\frac{π}{2}+2kπ)$为减
对称中心	$(\frac{kπ}{2},0)$	$(\frac{π}{2}+kπ,0)$	$(kπ,0)$

2. 三角函数公式

• 基本公式

• • $sec^2x=tan^2x+1$
• • $csc^2x=cot^2x+1$
• • $sin^2x+cos^2x=1$
• • $tanx=\frac{sinx}{cosx}$
• • $cotx=\frac{cosx}{sinx}$
• • $secx=\frac{1}{cosx}$
• • $cscx=\frac{1}{sinx}$
• • $sinx+cosx=√2sin(x+\frac{π}{4})$
• • $sinx-cosx=√2sin(x-\frac{π}{4})$

• 诱导公式

角\函数	sin	cos	tan	cot
-x	-sinx	cosx	-tanx	-cotx
$\frac{π}{2}-x$	cosx	sinx	cotx	tanx
$\frac{π}{2}+x$	cosx	-sinx	-cotx	-tanx
π-x	sinx	-cosx	-tanx	-cotx
π+x	-sinx	-cosx	cotx	tanx
$\frac{3π}{2}-x$	-cosx	-sinx	cotx	tanx
$\frac{3π}{2}+x$	-cosx	sinx	-cotx	-tanx
2π-x	-sinx	cosx	-tanx	-cotx
2π+x	sinx	cosx	tanx	cotx

• • $sin(π±t)=∓sint$
• • $cos(π±t)=-cost$
• • $sin(\frac{π}{2}±t)=cost$
• • $cos(\frac{π}{2}±t)=∓sint$

• 降幂公式

• • $sin^2x=\frac{1-cos2x}{2}$
• • $cos^2x=\frac{1+cos2x}{2}$
• • $tan^2x=\frac{1-cos2x}{1+cos2x}$

• 倍角公式

• • $sin2x=2sinxcosx$
• • $cos2x=cos^2x-sin^2x=2cos^2x-1=1-2sin^2x$
• • $tan2x=\frac{2tanx}{1-tan^2x}$
• • $tan\frac{x}{2}=\frac{sinx}{1+cosx}=\frac{1-cosx}{sinx}=cscx-cotx$

• 和差公式

• • $sin(x±y)=sinxcosy±cosxsiny$
• • $cos(x±y)=cosxcosy∓sinxsiny$
• • $tan(x±y)=\frac{tanx±tany}{1∓tanxtany}$
• • $cot(x±y)=\frac{cotxcoty∓1}{coty±cotx}$

• 和差化积公式

• • $sin\alpha+sin\beta=2sin(\frac{\alpha+\beta}{2})cos(\frac{\alpha-\beta}{2})$
• • $sin\alpha-sin\beta=2cos(\frac{\alpha+\beta}{2})sin(\frac{\alpha-\beta}{2})$
• • $cos\alpha+cos\beta=2cos(\frac{\alpha+\beta}{2})cos(\frac{\alpha-\beta}{2})$
• • $cos\alpha-cos\beta=-2sin(\frac{\alpha+\beta}{2})sin(\frac{\alpha-\beta}{2})$

• 积化和差公式

• • $sin\alpha sin\beta=\frac{1}{2}[cos(\alpha-\beta)-cos(\alpha+\beta)]$
• • $cos\alpha cos\beta=\frac{1}{2}[cos(\alpha-\beta)+cos(\alpha+\beta)]$
• • $sin\alpha cos\beta=\frac{1}{2}[sin(\alpha+\beta)+sin(\alpha-\beta)]$

• 万能公式

• • $sinx=\frac{2tan\frac{x}{2}}{1+tan^2\frac{x}{2}}$
• • $cosx=\frac{1-tan^2\frac{x}{2}}{1+tan^2\frac{x}{2}}$
• • $tanx=\frac{2tan\frac{x}{2}}{1-tan^2\frac{x}{2}}$

---

常见不等式与数列

1. 常见不等式

• 三角不等式:
• • $||a|-|b||≤|a±b|≤|a|+|b|$
• 算数不等式:
• • $a^2+b^2≥2ab$
• • $|ab|≤\frac{a^2+b^2}{2}$
• • a≥0时:
• • $\frac{a_1+a_2+…+a_n}{n}≥^n√{a_1a_2…a_n}$
• 柯西不等式:
• • $(a_1^2+a_2^2+…+a_n^2)(b_1^2+b_2^2+…+b_n^2)≥(a_1b_1+a_2b_2+…+a_nb_n)^2$

2. 常见数列

---

函数的初等特性

1. 有界性: 设$y=f(x)$,若存在常数M>0,使得对于定义域D内的任意x,有$|f(x)|≤M$,则称f(x)在D上有界

• 有界的充分必要条件是函数的值域有上界和下界

2. 单调性：设$y=f(x)$,若对于定义域D内的任意$x_1,x_2$,当$x_1 < x_2$时,有$f(x_1) < f(x_2)$,则称f(x)在D上单调递增；若对于定义域D内的任意$x_1,x_2$,当$x_1 < x_2$时,有$f(x_1) > f(x_2)$,则称f(x)在D上单调递减

3. 奇偶性：设$y=f(x)$,定义域D关于原点对称，若对于定义域D内的任意x,有$f(-x)=-f(x)$,则称f(x)为奇函数；若对于定义域D内的任意x,有$f(-x)=f(x)$,则称f(x)为偶函数

4. 周期性：设$y=f(x)$,若存在常数T>0,使得对于定义域D内的任意x和$x±T$，有$f(x)=f(x±T)$,则称f(x)为周期函数，T为函数f(x)的周期

1.2 极限

1.2.1 极限的定义

1. 极限

• x → a ：x趋于a,不能等于a，且从左右两侧趋近...