Everything is difficult until you know how to do it.

Hi，同学们，上周我们学习了统计学基础知识，包括概率基础、描述统计学和推论统计学的基础知识，本周我们将会进一步学习推论统计学——置信区间&假设检验以及它们的应用之一A/B-test，在这之后，我们还会讲解一部分机器学习入门——线性回归&逻辑回归，与上周相比，这周我们会接触较深的理论知识，更多的代码，你可能会觉得学起来有些吃力，但请一定保持信心，你可以多次暂停观看课程中的讲解视频，跟着一起多动手，或者你也可以按照下面我给出的额外资料去查漏补缺，相信你们一定可以的！

项目四(P4)阶段总共包含三周，在这三周内，我们要对统计学进行学习，掌握基础的描述统计学理论、基本的概率知识、二项分布和贝叶斯公式，并学会使用 Python 来实践；学习正态分布、抽样分布、置信区间以及假设检验的概念和计算方式；学习线性回归以及逻辑回归，在真实场景中应用，比如分析 A/B 测试结果，搭建简单的监督机器学习模型。可谓是时间紧任务重，但是也别怕，统计学的基础知识还是非常简单的，跟着课程内容一步步来，自己多做笔记多查资料，一定没问题的！

那么我们的课程安排：

本阶段可能是个挑战，请一定要保持自信，请一定要坚持学习和总结，如果遇到任何课程问题请参照如下顺序进行解决：

• 先自行查找问题答案（注意提取关键词），参考：谷歌/必应搜索、CSDN、stackoverflow
• 额外参考资料：
  • 可汗学院概率论与统计课程
  • 机会的数学-陈希孺
  • 条件概率及全概率公式及贝叶斯公式
  • statistics for data science
• 若问题未解决，请将问题及其所在课程章节发送至微信群，并@助教即可

饭要一口一口吃，路要一步一步走，大家不要被任务吓到，跟着导学一步一步来，肯定没问题哒！那我们开始吧！

注：本着按需知情原则，所涉及的知识点都是在数据分析过程中必须的、常用的，而不是最全面的，想要更丰富，那就需要你们课下再进一步的学习和探索！

本周目标

学习课程中的置信区间 - 逻辑回归课程，掌握统计学进阶知识。

学习计划

知识清单

置信区间

学习之前可以先回顾一下正态分布、抽样分布和中心极限定理的相关知识。

是什么

还记得上周用到的优达学生喝咖啡的数据吗？我们同样以此为例来探讨下置信区间是什么。

假设，优达的学生有数十万个（总体），而我们能获得的学生数据只有几百个（样本），我们通过做样本均值进行抽样分布，得到了一个近似正态分布的图形，但这也仅仅是样本的均值分布，也就是样本统计量。我们利用样本统计量的分布去构造总体均值（总体参数）的估计区间，就叫做置信区间。

有什么

• 置信区间的两种应用

  • 刚才的举例中我们用得是“均值”，这算是利用抽样分布建立单个参数的置信区间，可以应用在单变量估计等方面；

  • 你还可以计算两种分类之间均值的差，这就是两个参数的置信区间，可以用在两变量的对比(A/B-Test)上，比如说医学上不同药物的治疗效果，不同广告的吸金率，不同网页的点击率等等。

• 置信区间的显著性

  • 统计显著性：即我们通过理论分析得到的结果。在统计学上用α表示，叫做显著性水平，它表达的是区间估计的不可靠概率。比如说，我们获取了95%的置信区间，那么显著性水平α = 1 - P = 5%。

    一般的，显著性水平都要求达到5%即可，这在之后的假设检验中会学习到。

  • 实际显著性：即我们除了理论分析得到的结果外，还要考虑实际情况，比如说你能有多少资金用于投资，或者你的网站承载力能达到多少等。

• 与传统置信区间方法的对比

  传统的置信区间/假设检验方法有很多，比如说t-检验、双边t-检验等等，但是我们所掌握的自助取样法可以代替他们全部，当然有一个前提条件，那就是你的样本容量一定要足够大，如果你的样本容量实在是少，那就只能选择传统方法去处理了。

  获取传统方法python代码的方法，请自行去Stackoverflow搜索。

• 准确性&可靠性

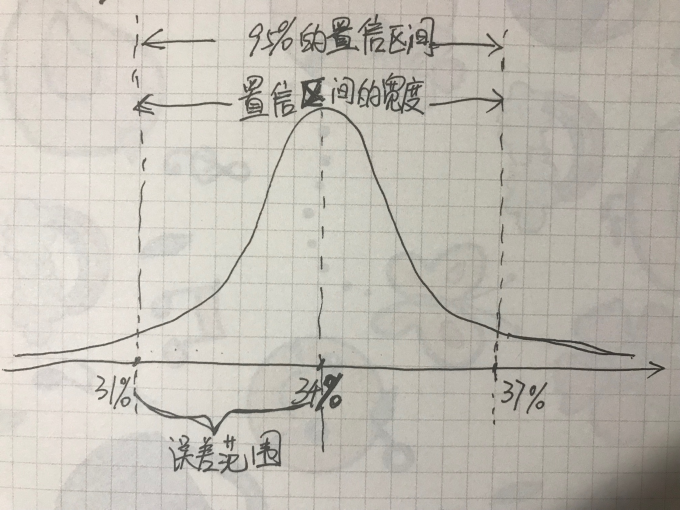
  这里课程中翻译的有点儿晦涩，这里着重讲一下，我们以候选人A为例（在95%可靠性下具有34%±3%的支持率），大概分布可以如下所示：字丑就将就着点看吧。。。

  

  • 在上图中我们能发现，置信区间的置信概率（可靠性）越高，置信区间的宽度也就越宽，误差范围（准确性）也就会越大；那么当我们缩小误差范围时，置信区间的宽度和可靠性也就随之降低。
  • 结论：置信区间的准确性和可靠性是一对相互矛盾的标准，所以在实际工作中，只能提出其中一个条件，然后推求另一条件的变动情况，如果所推求的另一条件不能满足要求，就应该考虑增加样本容量，重新进行抽样，直至符合要求为止。

怎么用

课程中已经给出了很好的示例、问题及解答，在这里只是拎出一些面生的代码进行讲解。

1
2
3
4
5
6

#设置随机种子，能保证结果之后可以复现
np.random.seed(7)
#按百分比取值
np.percentile(array,q)#q介于0到100，取的是array中的q%位置的数。（从小至大排序）
#拓展——按分位数取值，其实效果和上面按百分比取值一样，只是q值的范围变了
np.quantile(array,q)#q介于0到1，取的是array中的q位置的数。

注意：置信区间和假设检验只关注的是总体参数，而不能对某一个体下结论。

假设检验

是什么

• 基本概念

刚才我们讲解了什么是置信区间——为了得到总体指标，使用样本统计量去估计总体参数——这是一个从样本出发去研究总体的过程。

我们现在换一个角度，在实际分析问题中，能否去假定...