在计算物体旋转时，如相机标定中的旋转矩阵R，通常都是以三维矩阵表示，三个自由度分别是绕三个坐标轴的旋转角度，但在Unity中，或者像colmap中,都是以四元数(Quaternion)来表示三维旋转的。实际上是复平面向量与实数域矩阵的一个转换关系，这里推导一下。

二维情况

一维数轴上的复数对应于一个二维实数空间，比如一个二维空间坐标为 $(x,y)$ 的复数表示为 $x + yi$ 。
给定两个复数 $z1 = a + bi$, $z2 = c +di$, 其乘积可以表示为:
$$ z1z2 = (a+bi)(c+di) = (ac-bd)+(ad+bc)i $$
对于向量$z2$,与$z1$的乘积可以表示为矩阵形式，即：
$$
\begin{bmatrix}
a & -b \\
b & a \\
\end{bmatrix}
\cdot z2
$$
如果将$z2$也看做一个变换表示成矩阵形式，则
$$
z1z2 =
\begin{bmatrix}
a & -b \\
b & a \\
\end{bmatrix}
\cdot
\begin{bmatrix}
c & -d \\
d & a \\
\end{bmatrix}
$$

此时满足交换律。

二维旋转

设向量模长为1，即$\sqrt[2]{a^2 + b ^2} =1$，则$a = cos\theta, b=sin\theta$, 则对一个向量$\vec{v}=x+yi$,其乘积为$\vec{v} \dot z = (xcos\theta -ysin\theta) +(xsin\theta +ycos\theta)i$,

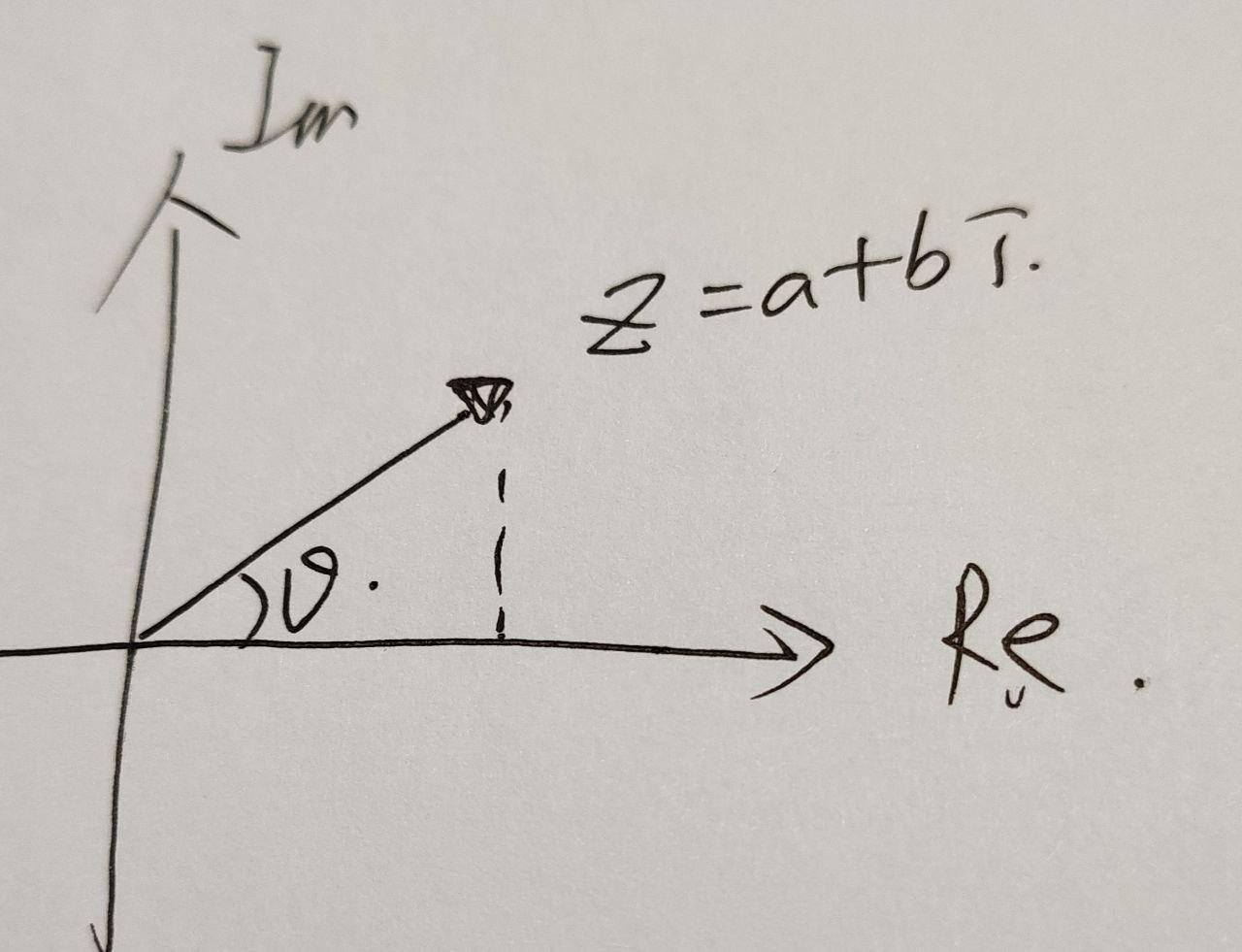
设向量$\vec{v}$的模为r，则$\vec{v}\cdot \vec{z} = r(cos\theta_1cos\theta_2 -sin\theta_1sin\theta_2)+r(cos\theta_1sin\theta_1 + sin\theta_1cos\theta_2)i = rcos(\theta_1 +\theta_2) +rsin(\theta_1 + \theta_2) i $
可以看出，一个单位的二维向量，或一维复数，可以表示成一个旋转变换，即逆时针旋转$\theta$角。

所以二维的旋转矩阵可以很直观的求得:
$$
\begin{bmatrix}
cos\theta & -sin\theta \\
sin\theta & cos\theta \\
\end{bmatrix}
$$

极坐标形式

其实将复数表示成极坐标形式，欧拉公式将三角函数和复平面关联起来，于是可以很直接的将$ e^{i\theta} = cos\theta + isin\theta$带入，角度旋转即$$ e^{i\theta_1} * e^{i\theta_2} = e^{i(\theta_1 + \theta_2)}$$

三维情况

先看向量的旋转: 将向量$\vec{v}$绕旋转轴$\vec{u}$旋转$\theta$角。
将$\vec{v}$分解成两个正交向量的和，分别是平行于$\vec{u}$和垂直于$\vec{u}$的向量，记为$\vec{v_{||}}$和$\vec{v_\bot}$,平行的向量旋转不变，因此只需要考虑垂直向量即可。
对于$\vec{v_{||}}$，其实就是在$\vec{u}$上的正交投影，因此有$\vec{v_{||}} = \frac{\vec{u}\cdot \vec{v}}{||\vec{u}||^2} \vec{u}$,设$\vec{u}$为单位向量，则可以表示为$\vec{v_{||}} = (\vec{u}\cdot...